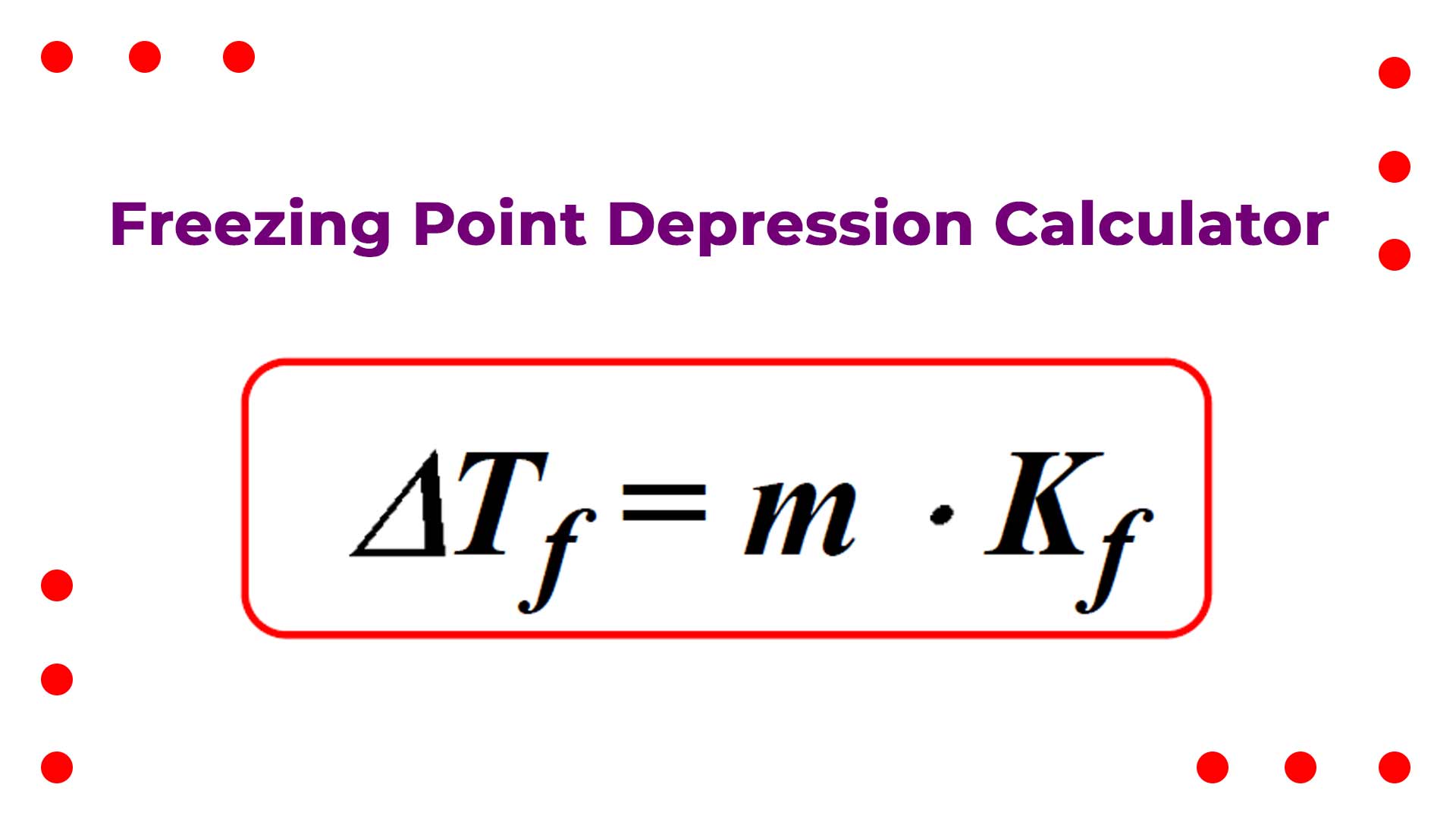Introducing our Freezing Point Depression Calculator. Explore the fascinating world of freezing point depression and its impact on various solvents. Discover how adding solutes affects freezing points and utilize our interactive calculator to determine freezing point changes across a range of solvents. Uncover the science behind this phenomenon and its practical applications in everyday life. Let’s delve into the depths of freezing point depression together!
What is a Freezing Point Depression Calculator?
A Freezing Point Depression Calculator is a tool used to estimate and calculate the decrease in the freezing point temperature of a solution when a nonvolatile solute is added to a solvent. This phenomenon is known as freezing point depression.
When a solute is added to a solvent, it disrupts the regular arrangement of solvent molecules in the solid state, making it more difficult for the solution to freeze. As a result, the freezing point of the solution becomes lower than that of the pure solvent.
The calculator typically requires input values such as:
- Molality (moles of solute per kilogram of solvent)
- Freezing point depression constant (specific to the solvent)
- Freezing point of the pure solvent
Using these inputs, the calculator applies the freezing point depression formula, which involves the relationship between molality, depression constant, and the change in freezing point. It then calculates the freezing point depression and the new freezing point of the solution.
The freezing point depression calculator is particularly useful in various practical applications, such as determining the appropriate antifreeze mixture for car radiators, predicting the freezing point of brine used for de-icing roads, and understanding the freezing properties of solutions in different scenarios.
The calculator allows users to quickly and conveniently perform these calculations without the need for manual equations, making it a valuable tool for chemists, engineers, and anyone dealing with solutions and temperature-dependent processes.
How does this Freezing Point Depression Calculator work?
The Freezing Point Depression Calculator works based on the principles of colligative properties, specifically freezing point depression. Colligative properties are characteristics of solutions that depend solely on the number of solute particles present, rather than the specific identity of the solute particles.
Here’s how the calculator works step by step:
- Input Parameters:
- Molality (m): The amount of solute in moles per kilogram of solvent. So the user has to input the Molality.
- Freezing Point Depression Constant (Kf): A constant specific to the solvent that represents the change in freezing point for a 1-molal solution. Below we have given some Freezing points depression constant values for several solvents. You can use them for convenience.
- Freezing Point of Pure Solvent (Tf0): The temperature at which the pure solvent freezes.
- Calculation of Freezing Point Depression (ΔTf): The calculator first calculates the freezing point depression (ΔTf) using the formula:ΔTf = Kf * mWhere:
- ΔTf is the change in freezing point temperature of the solution.
- Kf is the freezing point depression constant.
- m is the molality of the solution.
- Calculation of Solution Freezing Point (Tfs): The new freezing point of the solution (Tfs) is calculated using the formula: Tfs = Tf0 – ΔTf Where:
- Tfs is the freezing point of the solution.
- Tf0 is the freezing point of the pure solvent.
- ΔTf is the freezing point depression.
- Display of Results: The calculator then displays the calculated freezing point depression (ΔTf) and the new freezing point of the solution (Tfs).
The freezing point depression occurs because the presence of solute particles disrupts the regular crystal lattice formation of the solvent molecules as they transition from the liquid to the solid state. This disruption requires the solution to be cooled to a lower temperature than the pure solvent in order to freeze.
The calculator simplifies this process and allows users to quickly estimate the freezing point depression and the new freezing point of the solution based on the provided inputs. It is a valuable tool for various practical applications, such as antifreeze formulation, predicting brine freezing points, and understanding the behavior of solutions in temperature-dependent processes.
What is the value of Freezing Point Depression Constant (Kf)?
The value of the Freezing Point Depression Constant (Kf) varies depending on the solvent you are considering. Each solvent has its own unique Kf value, which represents how much the freezing point of that solvent is lowered when a certain amount of solute is added to it.
Here are some Kf values for a few common solvents:
- Water (H2O): Kf ≈ 1.86 °C·kg/mol
- Benzene (C6H6): Kf ≈ 5.12 °C·kg/mol
- Ethanol (C2H5OH): Kf ≈ 1.99 °C·kg/mol
- Chloroform (CHCl3): Kf ≈ 4.68 °C·kg/mol
- Ether (C4H10O): Kf ≈ 1.79 °C·kg/mol
These values represent the freezing point depression constant for a 1-molal solution of a nonvolatile solute in the respective solvents. Remember that these values are approximate and may vary slightly depending on conditions and experimental measurements.
The table on freezing point depression
| Solvent | Kf (°C·kg/mol) | ∆Tf (°C) | Tfs (°C) |
|---|---|---|---|
| Water | 1.86 | 0.10 | -0.10 |
| Ethanol | 1.99 | 0.20 | -0.20 |
| Acetone | 1.71 | 0.30 | -0.30 |
| Benzene | 5.12 | 0.40 | -0.40 |
| Toluene | 5.08 | 0.50 | -0.50 |
| Chloroform | 4.68 | 0.60 | -0.60 |
| Carbon Disulfide | 2.35 | 0.70 | -0.70 |
| Cyclohexane | 20.0 | 0.80 | -0.80 |
| Diethyl Ether | 1.26 | 0.90 | -0.90 |
| Acetic Acid | 3.07 | 1.00 | -1.00 |
| Formic Acid | 3.78 | 1.10 | -1.10 |
| Methanol | 1.86 | 1.20 | -1.20 |
| Propionic Acid | 3.60 | 1.30 | -1.30 |
| Nitrobenzene | 8.64 | 1.40 | -1.40 |
| Aniline | 5.90 | 1.50 | -1.50 |
| Glycerol | 20.7 | 1.60 | -1.60 |
| Phenol | 7.40 | 1.70 | -1.70 |
| Camphor | 40.0 | 1.80 | -1.80 |
| Naphthalene | 6.80 | 1.90 | -1.90 |
| Acetamide | 4.23 | 2.00 | -2.00 |
| Urea | 1.86 | 2.10 | -2.10 |
| Hydroquinone | 7.90 | 2.20 | -2.20 |
| Anthracene | 9.0 | 2.30 | -2.30 |
| Maleic Acid | 8.61 | 2.40 | -2.40 |
| Benzoic Acid | 12.2 | 2.50 | -2.50 |
| Adipic Acid | 6.08 | 2.60 | -2.60 |
| Lauric Acid | 3.40 | 2.70 | -2.70 |
| Phenanthrene | 30.0 | 2.80 | -2.80 |
| Citric Acid | 1.66 | 2.90 | -2.90 |
| Ethylene Glycol | 1.86 | 3.00 | -3.00 |
| Sodium Chloride | 3.61 | 3.10 | -3.10 |
| Potassium Nitrate | 1.86 | 3.20 | -3.20 |
| Ammonium Nitrate | 1.86 | 3.30 | -3.30 |
| Sodium Nitrate | 1.86 | 3.40 | -3.40 |
| Potassium Thiocyanate | 1.86 | 3.50 | -3.50 |
| Uric Acid | 1.86 | 3.60 | -3.60 |
| Caffeine | 1.86 | 3.70 | -3.70 |
| Paraffin | 2.4 | 3.80 | -3.80 |
| Naphthalene | 6.80 | 3.90 | -3.90 |
| Camphor | 40.0 | 4.00 | -4.00 |
| Sulfanilic Acid | 1.85 | 4.10 | -4.10 |
| Adipic Acid | 6.08 | 4.20 | -4.20 |
| Benzoic Acid | 12.2 | 4.30 | -4.30 |
| Anthracene | 9.0 | 4.40 | -4.40 |
| Lauric Acid | 3.40 | 4.50 | -4.50 |
What is freezing point depression in terms of entropy?
Freezing point depression can be understood in terms of entropy changes within a solution. Entropy is a measure of the randomness or disorder of a system. When a solution freezes, its molecules or particles become more organized in a solid structure, resulting in a decrease in entropy. This decrease in entropy during freezing contributes to lowering the solution’s freezing point compared to that of the pure solvent.
Here’s how freezing point depression is related to entropy:
- Pure Solvent: In a pure solvent, the molecules are more disordered, with higher entropy. When the solvent freezes, its molecules become more structured and ordered, decreasing entropy.
- Solution: In a solution, the solvent molecules are mixed with solute particles, creating a more disordered and random arrangement of particles. This mixing leads to a higher entropy compared to the pure solvent.
- Freezing Point Depression: When a solute is added to the solvent, it disrupts the organization of the solvent molecules during freezing. The solute particles interfere with forming the regular crystal lattice of the solvent. As a result, the solution’s freezing point is lowered because the system requires less energy to transition from the disordered solution state to the ordered solid state.
In essence, freezing point depression occurs because the solvent and solute particles are more disordered in solution than in the pure or solute states. The transition to a more ordered solid state is less favoured in a disordered solution due to increased entropy associated with the solution state.
The need to overcome the higher entropy of the solution contributes to the decrease in the freezing point. It requires the system to lose less entropy during freezing, making the process energetically more favourable and leading to a lower freezing point than the pure solvent.
Source: Brightstrom
Is freezing point depression negative?
Yes, freezing point depression is negative. Freezing point depression refers to the phenomenon where the freezing point of a solution is lower than that of the pure solvent. When a nonvolatile solute is added to a solvent, the solute-solvent interactions disrupt the regular crystal lattice’s formation during freezing. This disruption leads to a lowering of the freezing point of the solution compared to the freezing point of the pure solvent.
Mathematically, freezing point depression (∆Tf) is expressed as the difference between the freezing point of the pure solvent (Tf°) and the freezing point of the solution (Tfs):
∆Tf = Tf° – Tfs
Since the freezing point of the pure solvent is higher than the solution’s freezing point, the freezing point depression (∆Tf) is a negative value. In other words, the solution’s freezing point is lower than that of the pure solvent, resulting in a negative temperature change (∆Tf) when the solute is added.
This negative change in freezing point is a characteristic property of solutions and is used in various practical applications, such as antifreeze solutions and road de-icing during winter.